Task1 区块链简介与以太坊入门介绍

一、区块链简介

1.1、区块链的本质

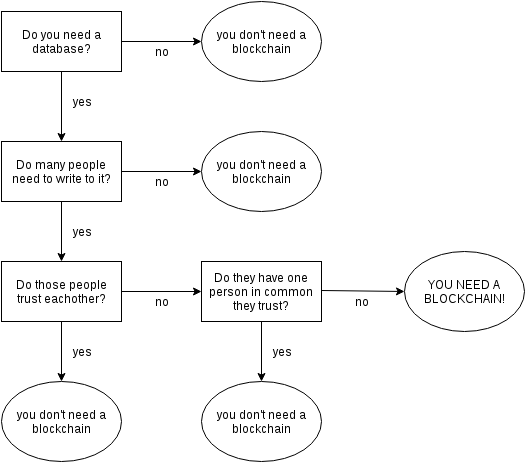
区块链，是一种特殊的分布式数据库，去中心化是其最大的特点。

去中心化一词，我是在美剧硅谷中第一次清楚地接触到，简单梳理下硅谷剧情，记忆不准确，参考博客

• 发散压缩算法 (Middle-Out Algorithm)
• 去中心化的互联网-New Internet
• 安东之子 Son of Anton

在正式的产品交付前几天，Richard 发现自己发送的加密信息，在 Morika 接受的短信中少了一个点，更严重的是，网络发送量和接受量不一致。最终推演的结果是，网络的加密算法被绕过或者被攻破了。加密算法可以说是世界上最重要的算法之一，如果说一旦有破解工具，一切隐私、安全都不存在。最终 Piper 创始人选择放弃，关上潘多拉魔盒。

说回正题，本文是作为一个区块链初学者的知识总结，参考了很多优秀的博客，文章框架按照学习思路汇总，在文章最后会附上参考资料链接。区块链的主要作用是储存信息。任何需要保存的信息，都可以写入区块链，也可以从里面读取，所以它是数据库。任何人都可以架设服务器，加入区块链网络，成为一个节点。区块链的世界里面，没有中心节点，每个节点都是平等的，都保存着整个数据库。你可以向任何一个节点，写入/读取数据，因为所有节点最后都会同步，保证区块链一致。

1.2、区块链的特点

分布式数据库并非新发明，市场上早有此类产品。但是，区块链有一个革命性特点。

区块链没有管理员，它是彻底无中心的。其他的数据库都有管理员，但是区块链没有。如果有人想对区块链添加审核，也实现不了，因为它的设计目标就是防止出现居于中心地位的管理当局。

正是因为无法管理，区块链才能做到无法被控制。否则一旦大公司大集团控制了管理权，他们就会控制整个平台，其他使用者就都必须听命于他们了。

但是，没有了管理员，人人都可以往里面写入数据，怎么才能保证数据是可信的呢？被坏人改了怎么办？请接着往下读，这就是区块链奇妙的地方。

1.3、区块链技术与算法

区块链技术不是单独的一项技术，而是一系列技术组成的技术栈，其具有以下的特点：

• 数据分布式存储
• 存储的数据不可逆、不可篡改、可回溯
• 数据的创建和维护由所有参与方共同参与

为了实现这些特点、维护区块链应用的稳定运行，区块链技术中包含了分布式存储技术、密码学技术、共识机制以及区块链2.0提出的智能合约。

1.3.1、区块

区块链由一个个区块（block）组成。区块很像数据库的记录，每次写入数据，就是创建一个区块。

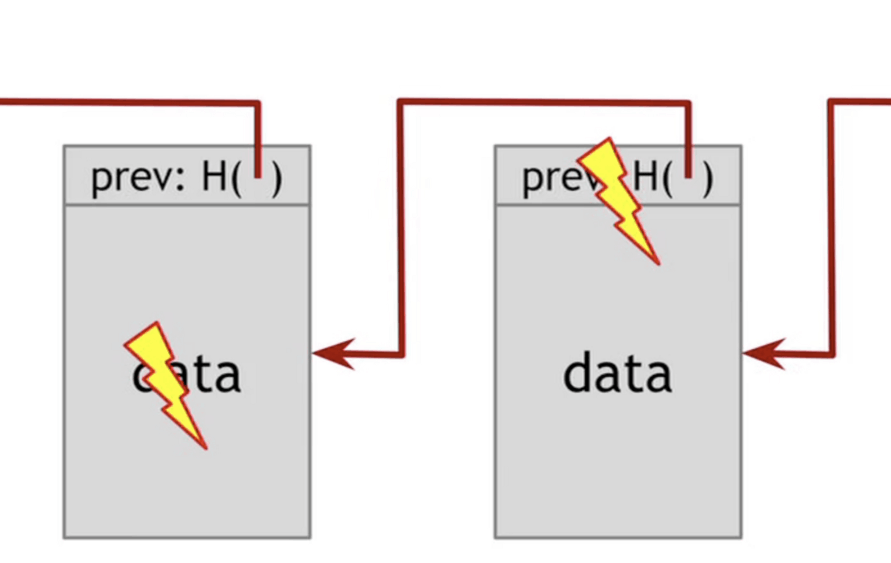
每个区块包含两个部分。

• 区块头（Head）：记录当前区块的特征值
• 区块体（Body）：实际数据

区块头包含了当前区块的多项特征值。

• 生成时间
• 实际数据（即区块体）的哈希
• 上一个区块的哈希
• …

这里，我们需要理解什么叫哈希（hash），这是理解区块链必需的。

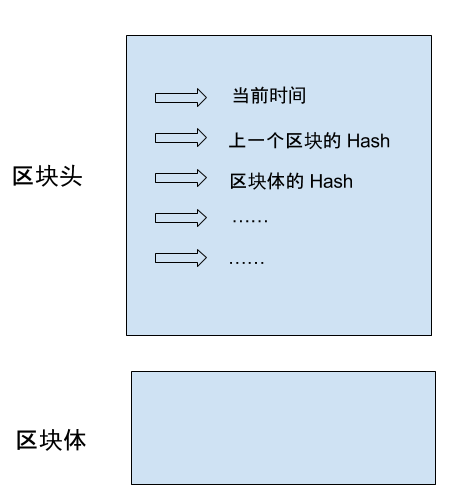
所谓”哈希”就是计算机可以对任意内容，计算出一个长度相同的特征值。区块链的哈希长度是256位，这就是说，不管原始内容是什么，最后都会计算出一个256位的二进制数字。而且可以保证，只要原始内容不同，对应的哈希一定是不同的。

举例来说，字符串123的哈希是a8fdc205a9f19cc1c7507a60c4f01b13d11d7fd0（十六进制），转成二进制就是256位，而且只有123能得到这个哈希。（理论上，其他字符串也有可能得到这个哈希，但是概率极低，可以近似认为不可能发生。）

因此，就有两个重要的推论。

• 推论1：每个区块的哈希都是不一样的，可以通过哈希标识区块。
• 推论2：如果区块的内容变了，它的哈希一定会改变。

1.3.2、Hash 的不可修改性

区块与哈希是一一对应的，每个区块的哈希都是针对”区块头”（Head）计算的。也就是说，把区块头的各项特征值，按照顺序连接在一起，组成一个很长的字符串，再对这个字符串计算哈希。

Hash = SHA256( 区块头 )

上面就是区块哈希的计算公式，SHA256是区块链的哈希算法。注意，这个公式里面只包含区块头，不包含区块体，也就是说，哈希由区块头唯一决定，

前面说过，区块头包含很多内容，其中有当前区块体的哈希，还有上一个区块的哈希。这意味着，如果当前区块体的内容变了，或者上一个区块的哈希变了，一定会引起当前区块的哈希改变。

这一点对区块链有重大意义。如果有人修改了一个区块，该区块的哈希就变了。为了让后面的区块还能连到它（因为下一个区块包含上一个区块的哈希），该人必须依次修改后面所有的区块，否则被改掉的区块就脱离区块链了。由于后面要提到的原因，哈希的计算很耗时，短时间内修改多个区块几乎不可能发生，除非有人掌握了全网51%以上的计算能力。

正是通过这种联动机制，区块链保证了自身的可靠性，数据一旦写入，就无法被篡改。这就像历史一样，发生了就是发生了，从此再无法改变。

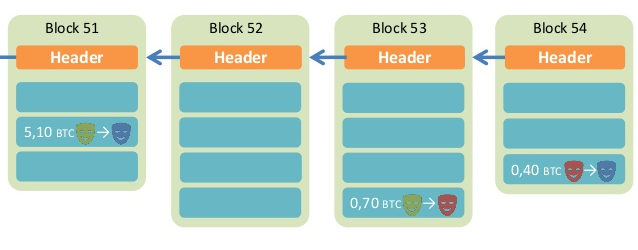
每个区块都连着上一个区块，这也是”区块链”这个名字的由来。

1.3.3、分布式存储技术

与传统的数据存储技术不同，在区块链技术中，数据并不是集中存放在某个数据中心上，也不是由某个权威机构或是大多数节点来存储，而是分散存储在区块链网络中的每一个节点上。

节点和区块的关系是什么？

可以用共享文档来简单描述：所有可以访问共享文档的账号就叫做节点，当然全节点需要同步共享文档，也就是拥有全部的区块数据区块就是共享文档。每个人更新了，所有人都可以查看最新的文档

1.3.4、密码学技术

为了实现数据的不可逆、不可篡改和可回溯，区块链技术采用了一系列密码学算法和技术，包括哈希算法、Merkle 树、非对称加密算法。

哈希算法

哈希算法是一个单向函数，可以将任意长度的输入数据转化为固定长度的输出数据（哈希值），哈希值就是这段输入数据唯一的数值表现。由于在计算上不可能找到哈希值相同而输入值不同的字符串，因此两段数据的哈希值相同，就可以认为这两段数据也是相同的，所以哈希算法常被用于对数据进行验证。

在区块链中，数据存储在区块里。每个区块都有一个区块头，区块头中存储了一个将该区块所有数据经过哈希算法得到的哈希值，同时，每个区块中还存储了前一个区块的哈希值，这样就形成了区块链。如果想要篡改某一个区块A中的数据，就会导致A的哈希值发生变化，后一个区块B就无法通过哈希值正确地指向A，这样篡改者又必须篡改B中的数据……也就是说，篡改者需要篡改被篡改的区块以及后面的所有区块，才能让所有的节点都接受篡改。

Merkle树

Merkle树是一种树形结构，在区块链中，Merkle树的叶子节点是区块中数据的哈希值，非叶子节点是其子结点组合后的哈希值，这样由叶子节点开始逐层往上计算，最终形成一个Merkle根，记录在区块的头部，这样就可以保证每一笔交易都无法篡改。

Merkle 树

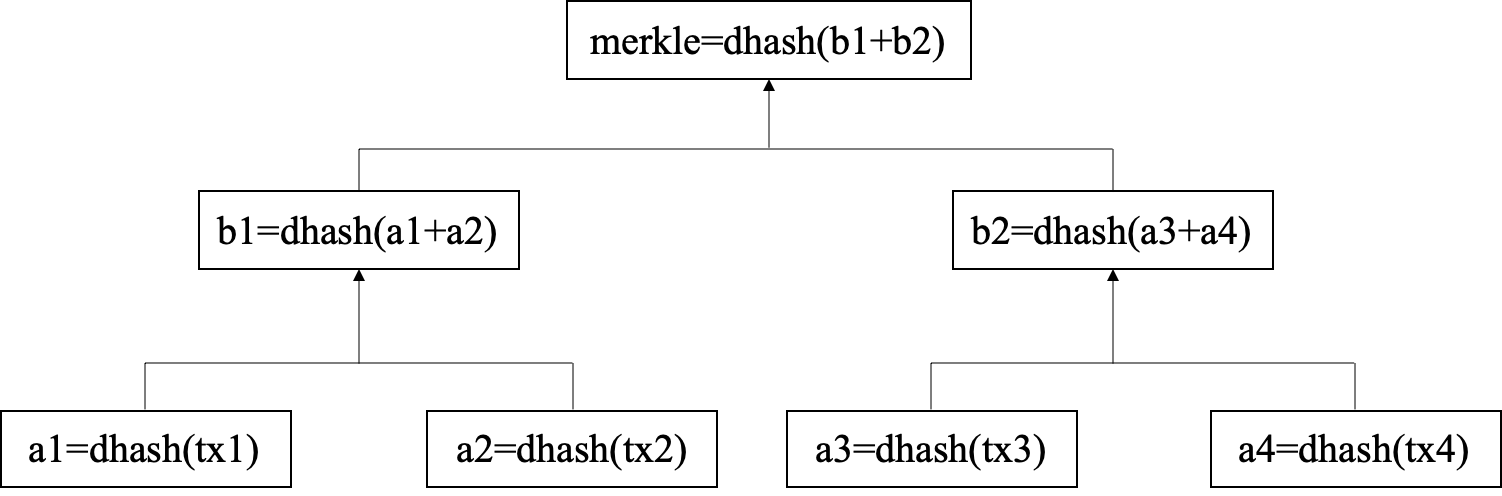
Merkle Tree实际上就是 树+Hash，具有树的性质，树的每个节点都是Hash值。Merkle Tree有以下特点：

1. Merkle Tree可以是二叉树，也可以是多叉树，不管是什么树，它都具有树结构的所有特点。
2. Merkel Tree的叶子节点的Value是数据集合的单元数据 或 单元数据的Hash值。
3. Merkel Tree所有非叶子节点的Value是所有子节点Value的Hash值。

Merkle Tree的应用

Merkel Tree多用在数据验证，其中最有名的应用领域可能就属加密货币了。矿机在挖矿实际上就是在运算一组复杂的公式：

SHA256(SHA256(version + prevHash + merkleRoot + time + currentDifficulty + nonce )) < TARGET

这里不必深究公式的意义，只需要关注其中的一个“merkleRoot”参数，这个“merkleRoot”就是Merkle Tree的根节点的值。想要算出根节点的值，必须要从叶子节点出发（在加密货币中，叶子节点通常为各区块内从n个交易提取的n个Hash值），最后由根节点的两个子节点的Hash计算出根节点的Hash。这只是挖矿的一个小环节。

Merkle Tree的实现

• 使用python语言，用到hashlib
• 为了简便，这里的Merkle Tree为二叉树
• 简单的将子节点Hash相加来生成父节点的Hash
• 假设初始有八个叶子节点，输出结果为二叉树各节点的值

import hashlib


class Merkle():  #Merkle Tree
    Merkle_tree = list([])
    
    def __init__(self, values):  # 将字符串初始化为叶子节点的Hash值
        child_node_start_index = len(values)
        total_length = len(values) * 2 - 1
        sha256 = hashlib.sha256()
        self.Merkle_tree = ["" for i in range(total_length)]
        
        for each in values:
            sha256.update(each.encode('utf-8'))
            self.Merkle_tree[child_node_start_index - 1] = sha256.hexdigest()
            child_node_start_index += 1
        
    def merkel_yourself(self):  # 生成Merkle Tree
        node_index = len(self.Merkle_tree) - 1  # 由叶子节点末尾向前计算非叶子节点的Hash
        sha256 = hashlib.sha256()
        
        while node_index > 0:
            sha256.update(self.Merkle_tree[node_index].encode('utf-8') + self.Merkle_tree[node_index - 1].encode('utf-8'))
            self.Merkle_tree[node_index // 2 - 1] = sha256.hexdigest()
            node_index -= 2
        
    def show_yourself(self):
        for each in self.Merkle_tree:
            print(each)
    

def main():
    values = list([])  # 测试数据
    values.append("Terence")
    values.append("Terence1023")
    values.append("TerenceCai")
	values.append("Don't forget me, I beg") 
    values.append("I'll remember you said") 
    values.append("Sometime it lasts in love") 
    values.append("But sometimes it hurts instead")
    
    tree = Merkle(values=values)
    tree.merkel_yourself()
    tree.show_yourself()
    

if __name__ == "__main__":
    main()

非对称加密技术

非对称加密技术使用两个非对称密钥：公钥和私钥。公钥和私钥具有两个特点：

1. 通过其中一个密钥加密信息后，使用另一个密钥才能解开
2. 公钥一般可以公开，私钥则保密

在区块链中，非对称加密技术主要用于信息加密、数字签名和登录认证。在信息加密场景中，信息发送者A使用接收者B提供的公钥对信息进行加密，B收到加密的信息后再通过自己的私钥进行解密。再数字签名场景中，发送者A通过自己的私钥对信息进行加密，其他人通过A提供的公钥来对信息进行验证，证明信息确实是由A发出。在登录认证场景中，客户端使用私钥加密登录信息后进行发送，其他人通过客户端公钥来认证登录信息。

• RSA 算法

  ​ RSA加密算法是最常用的非对称加密算法，CFCA在证书服务中离不了它。但是有不少新来的同事对它不太了解，恰好看到一本书中作者用实例对它进行了简化而生动的描述，使得高深的数学理论能够被容易地理解。
  ​ RSA是第一个比较完善的公开密钥算法，它既能用于加密，也能用于数字签名。RSA以它的三个发明者Ron Rivest, Adi Shamir, Leonard Adleman的名字首字母命名，这个算法经受住了多年深入的密码分析，虽然密码分析者既不能证明也不能否定RSA的安全性，但这恰恰说明该算法有一定的可信性，目前它已经成为最流行的公开密钥算法。
  　　RSA的安全基于大数分解的难度。其公钥和私钥是一对大素数（100到200位十进制数或更大）的函数。从一个公钥和密文恢复出明文的难度，等价于分解两个大素数之积（这是公认的数学难题）。

• ECC 椭圆曲线算法

  具体可以参见此文章：ECC椭圆曲线加密算法：介绍

1.3.5、非对称加密技术——RSA 算法

所谓非对称加密，其实很简单，就是加密和解密需要两把钥匙：一把公钥和一把私钥。

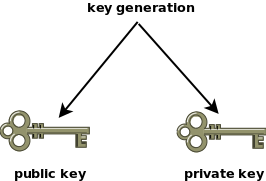
公钥是公开的，任何人都可以获取。私钥是保密的，只有拥有者才能使用。他人使用你的公钥加密信息，然后发送给你，你用私钥解密，取出信息。反过来，你也可以用私钥加密信息，别人用你的公钥解开，从而证明这个信息确实是你发出的，且未被篡改，这叫做数字签名。

RSA 算法原理

1.加密历史

1976年以前，所有的加密方法都是同一种模式：

　　（1）甲方选择某一种加密规则，对信息进行加密；

　　（2）乙方使用同一种规则，对信息进行解密。

由于加密和解密使用同样规则（简称”密钥”），这被称为“对称加密算法”（Symmetric-key algorithm）。

这种加密模式有一个最大弱点：甲方必须把加密规则告诉乙方，否则无法解密。保存和传递密钥，就成了最头疼的问题。

1976年，两位美国计算机学家Whitfield Diffie 和 Martin Hellman，提出了一种崭新构思，可以在不直接传递密钥的情况下，完成解密。这被称为“Diffie-Hellman密钥交换算法”。这个算法启发了其他科学家。人们认识到，加密和解密可以使用不同的规则，只要这两种规则之间存在某种对应关系即可，这样就避免了直接传递密钥。

这种新的加密模式被称为”非对称加密算法”。

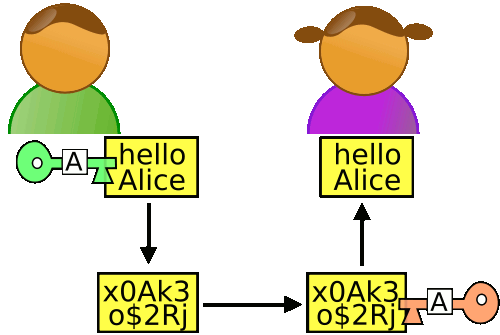
　　（1）乙方生成两把密钥（公钥和私钥）。公钥是公开的，任何人都可以获得，私钥则是保密的。

　　（2）甲方获取乙方的公钥，然后用它对信息加密。

　　（3）乙方得到加密后的信息，用私钥解密。

如果公钥加密的信息只有私钥解得开，那么只要私钥不泄漏，通信就是安全的。

1977年，三位数学家Rivest、Shamir 和 Adleman 设计了一种算法，可以实现非对称加密。这种算法用他们三个人的名字命名，叫做RSA算法。从那时直到现在，RSA算法一直是最广为使用的”非对称加密算法”。毫不夸张地说，只要有计算机网络的地方，就有RSA算法。

这种算法非常可靠，密钥越长，它就越难破解。根据已经披露的文献，目前被破解的最长RSA密钥是768个二进制位。也就是说，长度超过768位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024位的RSA密钥基本安全，2048位的密钥极其安全。

下面，我就进入正题，解释RSA算法的原理。文章共分成两部分，今天是第一部分，介绍要用到的四个数学概念。你可以看到，RSA算法并不难，只需要一点数论知识就可以理解。

2.互质关系

如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。

关于互质关系，不难得到以下结论：

　　1. 任意两个质数构成互质关系，比如13和61。

　　2. 一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3和10。

　　3. 如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57。

　　4. 1和任意一个自然数是都是互质关系，比如1和99。

　　5. p是大于1的整数，则p和p-1构成互质关系，比如57和56。

　　6. p是大于1的奇数，则p和p-2构成互质关系，比如17和15。

3.欧拉函数

请思考以下问题：

　　任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？（比如，在1到8之中，有多少个数与8构成互质关系？）

计算这个值的方法就叫做欧拉函数，以φ(n)表示。在1到8之中，与8形成互质关系的是1、3、5、7，所以 φ(n) = 4。

φ(n) 的计算方法并不复杂，但是为了得到最后那个公式，需要一步步讨论。

第一种情况

如果n=1，则 φ(1) = 1 。因为1与任何数（包括自身）都构成互质关系。

第二种情况

如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系。比如5与1、2、3、4都构成互质关系。

第三种情况

如果n是质数的某一个次方，即 n = p^k (p为质数，k为大于等于1的整数)，则

$$\phi\left(p^{k}\right)=p^{k}-p^{k-1}$$

比如 φ(8) = φ(2^3) =2^3 - 2^2 = 8 -4 = 4。

这是因为只有当一个数不包含质数p，才可能与n互质。而包含质数p的数一共有p^(k-1)个，即1×p、2×p、3×p、…、p^(k-1)×p，把它们去除，剩下的就是与n互质的数。

上面的式子还可以写成下面的形式：

$$\phi\left(p^{k}\right)=p^{k}-p^{k-1}=p^{k}\left(1-\frac{1}{p}\right)$$

可以看出，上面的第二种情况是 k=1 时的特例。

第四种情况

如果n可以分解成两个互质的整数之积，

　　n = p1 × p2

则

　　φ(n) = φ(p1p2) = φ(p1)φ(p2)

即积的欧拉函数等于各个因子的欧拉函数之积。比如，φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24。

这一条的证明要用到“中国剩余定理”，这里就不展开了，只简单说一下思路：如果a与p1互质(a<p1)，b与p2互质(b<p2)，c与p1p2互质(c<p1p2)，则c与数对 (a,b) 是一一对应关系。由于a的值有φ(p1)种可能，b的值有φ(p2)种可能，则数对 (a,b) 有φ(p1)φ(p2)种可能，而c的值有φ(p1p2)种可能，所以φ(p1p2)就等于φ(p1)φ(p2)。

第五种情况

因为任意一个大于1的正整数，都可以写成一系列质数的积。

$$n=p_{1}^{k_{1}} p_{2}^{k_{2} \ldots } p_{r}^{k_{r}}$$

根据第4条的结论，得到

$$\phi(n)=\phi\left(p_{1}^{k_{1}}\right) \phi\left(p_{2}^{k_{2}}\right) \ldots \phi\left(p_{r}^{k_{r}}\right)$$

再根据第3条的结论，得到

$$\phi(n)=p_{1}^{k_{1}} p_{2}^{k_{2} \ldots} p_{r}^{k_{r}}\left(1-\frac{1}{p_{1}}\right)\left(1-\frac{1}{p_{2}}\right) \ldots\left(1-\frac{1}{p_{r}}\right)$$

也就等于

$$\phi(n)=n\left(1-\frac{1}{p_{1}}\right)\left(1-\frac{1}{p_{2}}\right) \ldots\left(1-\frac{1}{p_{r}}\right)$$

这就是欧拉函数的通用计算公式。比如，1323的欧拉函数，计算过程如下：

$$\phi(1323)=\phi\left(3^{3} \times 7^{2}\right)=1323\left(1-\frac{1}{3}\right)\left(1-\frac{1}{7}\right)=756$$

4.欧拉定理

欧拉函数的用处，在于欧拉定理)。”欧拉定理”指的是：

如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：

$$a^{\phi(n)} \equiv 1(\bmod n)$$

也就是说，a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。比如，3和7互质，而7的欧拉函数φ(7)等于6，所以3的6次方（729）减去1，可以被7整除（728/7=104）。

欧拉定理的证明比较复杂，这里就省略了。我们只要记住它的结论就行了。

欧拉定理可以大大简化某些运算。比如，7和10互质，根据欧拉定理，

$$7^{\phi(10)} \equiv 1(\bmod 10)$$

已知 φ(10) 等于4，所以马上得到7的4倍数次方的个位数肯定是1。

$$7^{4 k} \equiv 1(\bmod 10)$$

因此，7的任意次方的个位数（例如7的222次方），心算就可以算出来。

欧拉定理有一个特殊情况。

假设正整数a与质数p互质，因为质数p的φ(p)等于p-1，则欧拉定理可以写成

$$a^{p-1} \equiv 1(\bmod p)$$

这就是著名的费马小定理。它是欧拉定理的特例。

欧拉定理是RSA算法的核心。理解了这个定理，就可以理解RSA。

5.模反元素

还剩下最后一个概念：

如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说ab被n除的余数是1。

$$a b \equiv 1(\bmod n)$$

这时，b就叫做a的“模反元素”。

比如，3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。显然，模反元素不止一个， 4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…}，即如果b是a的模反元素，则 b+kn 都是a的模反元素。

欧拉定理可以用来证明模反元素必然存在。

$$a^{\phi(n)} =aa^{\phi(n)-1}\equiv 1(\bmod n)$$

可以看到，a的 φ(n)-1 次方，就是a的模反元素。

6.密钥生成的步骤

我们通过一个例子，来理解RSA算法。假设爱丽丝要与鲍勃进行加密通信，她该怎么生成公钥和私钥呢？

第一步，随机选择两个不相等的质数p和q。

爱丽丝选择了61和53。（实际应用中，这两个质数越大，就越难破解。）

第二步，计算p和q的乘积n。

爱丽丝就把61和53相乘。

　　n = 61×53 = 3233

n的长度就是密钥长度。3233写成二进制是110010100001，一共有12位，所以这个密钥就是12位。实际应用中，RSA密钥一般是1024位，重要场合则为2048位。

第三步，计算n的欧拉函数φ(n)。

根据公式：

　　φ(n) = (p-1)(q-1)

爱丽丝算出φ(3233)等于60×52，即3120。

第四步，随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质。

爱丽丝就在1到3120之间，随机选择了17。（实际应用中，常常选择65537。）

第五步，计算e对于φ(n)的模反元素d。

所谓“模反元素”就是指有一个整数d，可以使得ed被φ(n)除的余数为1。

　　ed ≡ 1 (mod φ(n))

这个式子等价于

　　ed - 1 = kφ(n)

于是，找到模反元素d，实质上就是对下面这个二元一次方程求解。

$$e x+\varphi(n) y=1$$

已知 e=17, φ(n)=3120，

　　17x + 3120y = 1

这个方程可以用“扩展欧几里得算法”求解，此处省略具体过程。总之，爱丽丝算出一组整数解为 (x,y)=(2753,-15)，即 d=2753。

至此所有计算完成。

第六步，将n和e封装成公钥，n和d封装成私钥。

在爱丽丝的例子中，n=3233，e=17，d=2753，所以公钥就是 (3233,17)，私钥就是（3233, 2753）。

实际应用中，公钥和私钥的数据都采用ASN.1格式表达（实例）。

7.RSA算法的可靠性

回顾上面的密钥生成步骤，一共出现六个数字：

　　p
　　q
　　n
　　φ(n)
　　e
　　d

这六个数字之中，公钥用到了两个（n和e），其余四个数字都是不公开的。其中最关键的是d，因为n和d组成了私钥，一旦d泄漏，就等于私钥泄漏。

那么，有无可能在已知n和e的情况下，推导出d？

　　（1）ed≡1 (mod φ(n))。只有知道e和φ(n)，才能算出d。

　　（2）φ(n)=(p-1)(q-1)。只有知道p和q，才能算出φ(n)。

　　（3）n=pq。只有将n因数分解，才能算出p和q。

结论：如果n可以被因数分解，d就可以算出，也就意味着私钥被破解。

可是，大整数的因数分解，是一件非常困难的事情。目前，除了暴力破解，还没有发现别的有效方法。维基百科这样写道：

　　“对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。

　　假如有人找到一种快速因数分解的算法，那么RSA的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA密钥才可能被暴力破解。到2008年为止，世界上还没有任何可靠的攻击RSA算法的方式。

　　只要密钥长度足够长，用RSA加密的信息实际上是不能被解破的。”

举例来说，你可以对3233进行因数分解（61×53），但是你没法对下面这个整数进行因数分解。

　　12301866845301177551304949
　　58384962720772853569595334
　　79219732245215172640050726
　　36575187452021997864693899
　　56474942774063845925192557
　　32630345373154826850791702
　　61221429134616704292143116
　　02221240479274737794080665
　　351419597459856902143413

它等于这样两个质数的乘积：

　　33478071698956898786044169
　　84821269081770479498371376
　　85689124313889828837938780
　　02287614711652531743087737
　　814467999489
　　　　×
　　36746043666799590428244633
　　79962795263227915816434308
　　76426760322838157396665112
　　79233373417143396810270092
　　798736308917

事实上，这大概是人类已经分解的最大整数（232个十进制位，768个二进制位）。比它更大的因数分解，还没有被报道过，因此目前被破解的最长RSA密钥就是768位。

8.加密和解密

有了公钥和密钥，就能进行加密和解密了。

（1）加密要用公钥 (n,e)

假设鲍勃要向爱丽丝发送加密信息m，他就要用爱丽丝的公钥 (n,e) 对m进行加密。这里需要注意，m必须是整数（字符串可以取ascii值或unicode值），且m必须小于n。

所谓”加密”，就是算出下式的c：

　　me ≡ c (mod n)

爱丽丝的公钥是 (3233, 17)，鲍勃的m假设是65，那么可以算出下面的等式：

　　6517 ≡ 2790 (mod 3233)

于是，c等于2790，鲍勃就把2790发给了爱丽丝。

（2）解密要用私钥(n,d)

爱丽丝拿到鲍勃发来的2790以后，就用自己的私钥(3233, 2753) 进行解密。可以证明，下面的等式一定成立：

　　cd ≡ m (mod n)

也就是说，c的d次方除以n的余数为m。现在，c等于2790，私钥是(3233, 2753)，那么，爱丽丝算出

　　27902753 ≡ 65 (mod 3233)

因此，爱丽丝知道了鲍勃加密前的原文就是65。

至此，”加密—解密”的整个过程全部完成。

我们可以看到，如果不知道d，就没有办法从c求出m。而前面已经说过，要知道d就必须分解n，这是极难做到的，所以RSA算法保证了通信安全。

你可能会问，公钥(n,e) 只能加密小于n的整数m，那么如果要加密大于n的整数，该怎么办？有两种解决方法：一种是把长信息分割成若干段短消息，每段分别加密；另一种是先选择一种”对称性加密算法”（比如DES），用这种算法的密钥加密信息，再用RSA公钥加密DES密钥。

九、私钥解密的证明

最后，我们来证明，为什么用私钥解密，一定可以正确地得到m。也就是证明下面这个式子：

　　cd ≡ m (mod n)

因为，根据加密规则

　　ｍe ≡ c (mod n)

于是，c可以写成下面的形式：

　　c = me - kn

将c代入要我们要证明的那个解密规则：

　　(me - kn)d ≡ m (mod n)

它等同于求证

　　med ≡ m (mod n)

由于

　　ed ≡ 1 (mod φ(n))

所以

　　ed = hφ(n)+1

将ed代入：

　　mhφ(n)+1 ≡ m (mod n)

接下来，分成两种情况证明上面这个式子。

（1）m与n互质。

根据欧拉定理，此时

　　mφ(n) ≡ 1 (mod n)

得到

　　(mφ(n))h × m ≡ m (mod n)

原式得到证明。

（2）m与n不是互质关系。

此时，由于n等于质数p和q的乘积，所以m必然等于kp或kq。

以 m = kp为例，考虑到这时k与q必然互质，则根据欧拉定理，下面的式子成立：

　　(kp)q-1 ≡ 1 (mod q)

进一步得到

　　[(kp)q-1]h(p-1) × kp ≡ kp (mod q)

即

　　(kp)ed ≡ kp (mod q)

将它改写成下面的等式

　　(kp)ed = tq + kp

这时t必然能被p整除，即 t=t’p

　　(kp)ed = t’pq + kp

因为 m=kp，n=pq，所以

　　med ≡ m (mod n)

原式得到证明。

数字签名

数字签名是什么？

作者：David Youd

翻译：阮一峰

原文网址：http://www.youdzone.com/signature.html

1.

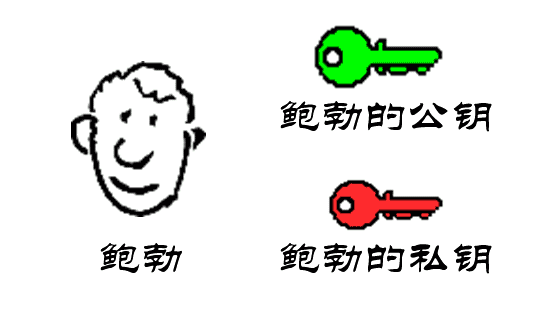
鲍勃有两把钥匙，一把是公钥，另一把是私钥。

2.

鲍勃把公钥送给他的朋友们——帕蒂、道格、苏珊——每人一把。

3.

苏珊要给鲍勃写一封保密的信。她写完后用鲍勃的公钥加密，就可以达到保密的效果。

4.

鲍勃收信后，用私钥解密，就看到了信件内容。这里要强调的是，只要鲍勃的私钥不泄露，这封信就是安全的，即使落在别人手里，也无法解密。

5.

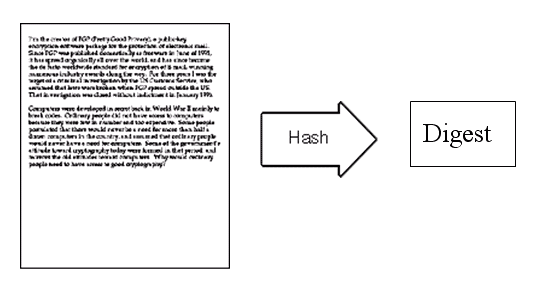
鲍勃给苏珊回信，决定采用”数字签名”。他写完后先用Hash函数，生成信件的摘要（digest）。

6.

然后，鲍勃使用私钥，对这个摘要加密，生成”数字签名”（signature）。

7.

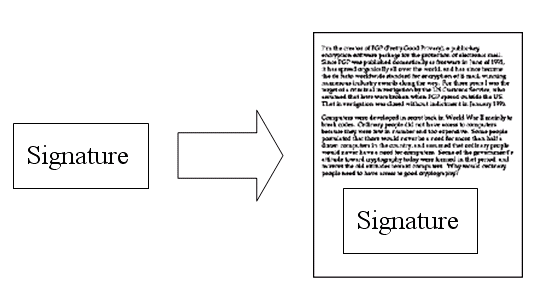
鲍勃将这个签名，附在信件下面，一起发给苏珊。

8.

苏珊收信后，取下数字签名，用鲍勃的公钥解密，得到信件的摘要。由此证明，这封信确实是鲍勃发出的。

9.

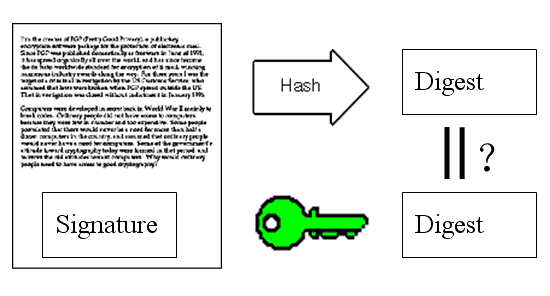
苏珊再对信件本身使用Hash函数，将得到的结果，与上一步得到的摘要进行对比。如果两者一致，就证明这封信未被修改过。

10.

复杂的情况出现了。道格想欺骗苏珊，他偷偷使用了苏珊的电脑，用自己的公钥换走了鲍勃的公钥。此时，苏珊实际拥有的是道格的公钥，但是还以为这是鲍勃的公钥。因此，道格就可以冒充鲍勃，用自己的私钥做成”数字签名”，写信给苏珊，让苏珊用假的鲍勃公钥进行解密。

11.

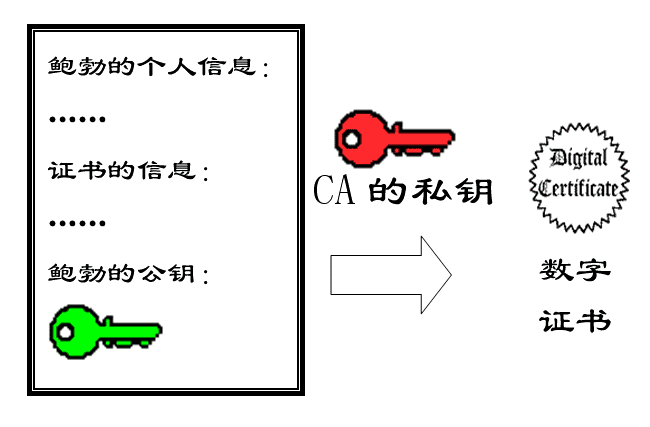
后来，苏珊感觉不对劲，发现自己无法确定公钥是否真的属于鲍勃。她想到了一个办法，要求鲍勃去找”证书中心”（certificate authority，简称CA），为公钥做认证。证书中心用自己的私钥，对鲍勃的公钥和一些相关信息一起加密，生成”数字证书”（Digital Certificate）。

12.

鲍勃拿到数字证书以后，就可以放心了。以后再给苏珊写信，只要在签名的同时，再附上数字证书就行了。

13.

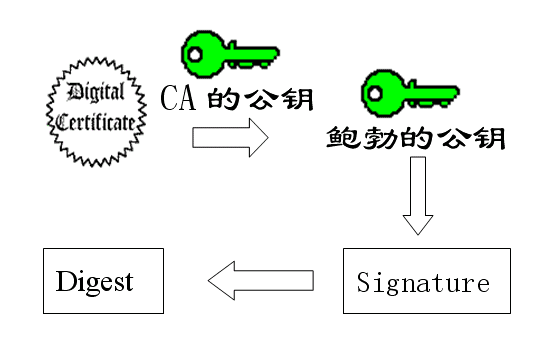
苏珊收信后，用CA的公钥解开数字证书，就可以拿到鲍勃真实的公钥了，然后就能证明”数字签名”是否真的是鲍勃签的。

14.

下面，我们看一个应用”数字证书”的实例：https协议。这个协议主要用于网页加密。

15.

首先，客户端向服务器发出加密请求。

16.

服务器用自己的私钥加密网页以后，连同本身的数字证书，一起发送给客户端。

17.

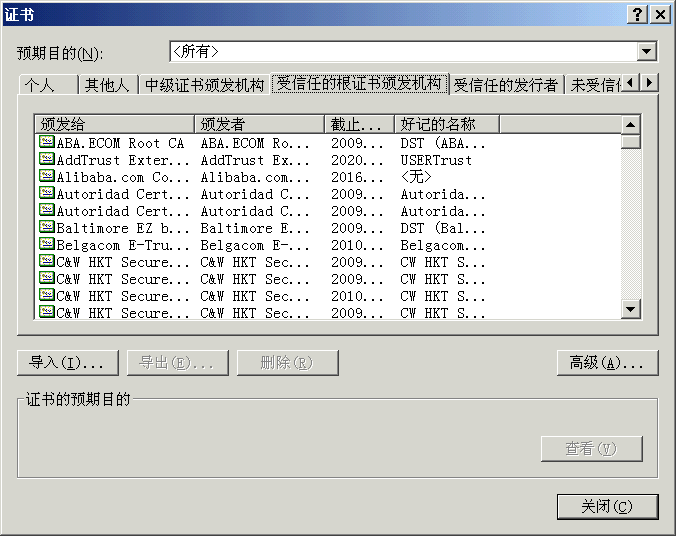
客户端（浏览器）的”证书管理器”，有”受信任的根证书颁发机构”列表。客户端会根据这张列表，查看解开数字证书的公钥是否在列表之内。

18.

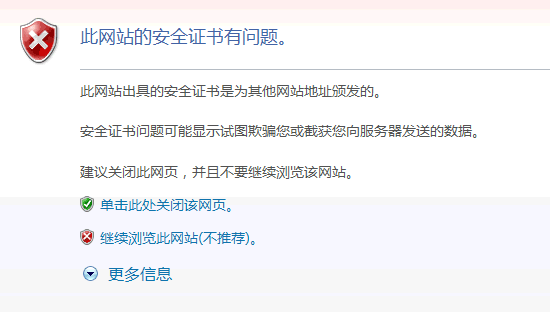
如果数字证书记载的网址，与你正在浏览的网址不一致，就说明这张证书可能被冒用，浏览器会发出警告。

19.

如果这张数字证书不是由受信任的机构颁发的，浏览器会发出另一种警告。

20.

如果数字证书是可靠的，客户端就可以使用证书中的服务器公钥，对信息进行加密，然后与服务器交换加密信息。

1.3.6、共识机制

区块链系统是一个分布式系统，分布式系统要解决都首要问题就是一致性问题，也就是如何使多个孤立的节点达成共识。在中心化系统中，由于有一个中心服务器这样的“领导”来统一各个节点，因此达成一致性几乎没有问题。但在去中心化场景下，由于各个节点是相互独立的，就可能会出现许多不一致的问题，例如由于网络状况等因素部分节点可能会有延迟、故障甚至宕机，造成节点之间通信的不可靠，因此一致性问题是分布式系统中一个很令人头疼的问题。

由 Eirc Brewer 提出，Lynch 等人证明的 CAP 定理为解决分布式系统中的一致性问题提供了思路。CAP 定理的描述如下：在分布式系统中，一致性、可用性和分区容错性三者不可兼得。这三个术语的解释如下：

• 一致性（Consistency）：所有节点在同一时刻拥有同样的值（等同于所有节点访问同一份最新的数据副本
• 可用性（Availability）：每个请求都可以在有限时间内收到确定其是否成功的响应
• 分区容错性（Partition tolerance）：分区是指部分节点因为网络原因无法与其他节点达成一致。分区容错性是指由网络原因导致的系统分区不影响系统的正常运行。例如，由于网络原因系统被分为 A, B, C, D 四个区，A, B 中的节点无法正常工作，但 C, D 组成的分区仍能提供正常服务。

在某些场景下，对一致性、可用性和分区容错性中的某一个特性要求不高时，就可以考虑弱化该特性，来保证整个系统的容错能力。区块链中常见的共识机制的基本思路正是来自 CAP 定理，部分区块链应用中用到的共识机制如下表：

共识机制	应用
PoW	比特币、莱特币、以太坊的前三个阶段
PoS	PeerCoin、NXT、以太坊的第四个阶段
PBFT	Hyperledger Fabric

PoW（Proof of Work，工作量证明）

PoW 机制的大致流程如下：

1. 向所有节点广播新交易和一个数学问题
2. 最先解决了数学问题的节点将交易打包成区块，对全网广播
3. 其他节点验证广播区块的节点是否解决了数学问题（完成了一定的工作量），验证通过则接受该区块，并将该区块的哈希值放入下一个区块中，表示承认该区块

由于在 PoW 机制中，区块的产生需要解决一个数学问题，也就是所谓的挖矿，这往往要消耗较大的算力和电力，因此节点们倾向于在最长的链的基础上添加区块，因为如果节点想在自己的链上添加新的区块，那么就需要重新计算 1 个或 $n$ 个这样的数学问题（每添加一个区块就需要计算一个）。因此在比特币中最长的链被认为是合法的链，这样节点间就形成了一套“共识”。

PoW 机制的优点是完全去中心化，缺点是需要依赖数学运算，资源的消耗会比其他的共识机制高，可监管性弱，同时每次达成共识需要全网共同参与运算，性能较低。

PoS（Proof of Stack，股权证明）

PoS 针对 PoW 的缺点做出了改进。PoS 要求参与者预先放置一些货币在区块链上用于换取“股权”，从而成为验证者（Validator），验证者具有产生区块的权利。PoS 机制会按照存放货币的量和时间给验证者分配相应的利息，同时还引入了奖惩机制，打包错误区块的验证者将失去他的股权——即投入的货币以及产生区块的权利。PoS 机制的大致流程如下：

1. 加入 PoS 机制的都是持币人，称为验证者
2. PoS 算法根据验证者持币的多少在验证者中挑选出一个给予产生区块的权利
3. 如果一定时间内没有产生区块，PoS 就挑选下一个验证者，给予产生区块的权利
4. 如果某个验证者打包了一份欺诈性交易，PoS 将剥夺他的股权

PoS 的优点在于：

1. 引入了利息，使得像比特币这样发币总数有限的通货紧缩系统在一定时间后不会“无币可发”
2. 引入了奖惩机制使节点的运行更加可控，同时更好地防止攻击
3. 与 PoW 相比，不需要为了生成新区块而消耗大量电力和算力
4. 与 PoW 相比，缩短了达成共识所需的时间

由于 PoS 机制需要用户已经持有一定数量的货币，没有提供在区块链应用创立初始阶段处理数字货币的方法，因此使用 PoS 机制的区块链应用会在发布时预先出售货币，或在初期采用 PoW，让矿工获得货币后再转换成 PoS，例如以太坊现阶段采用的是 PoW 机制，在第四阶段“宁静”（Serenity）中将过渡到 PoS。

拜占庭将军问题（Byzantine Generals Problem）

拜占庭将军问题是分布式网络中的通信容错问题，可以描述为：

一组拜占庭将军各领一支队伍共同围困一座城市。各支军队的行动策略限定为进攻或撤离两种。因为部分军队进攻而部分军队撤离可能会造成灾难性的后果，因此各将军决定通过投标来达成一致策略，即“共进退”。因为各将军位于城市不同方向，他们只能通过信使互相联系。在投票过程中每位将军都将自己的选择（进攻或撤退）通过信使分别通知其他所有将军，这样一来每位将军根据自己的投票和其他所有将军送来的信息就可以知道共同投票的结果，进而做出行动。

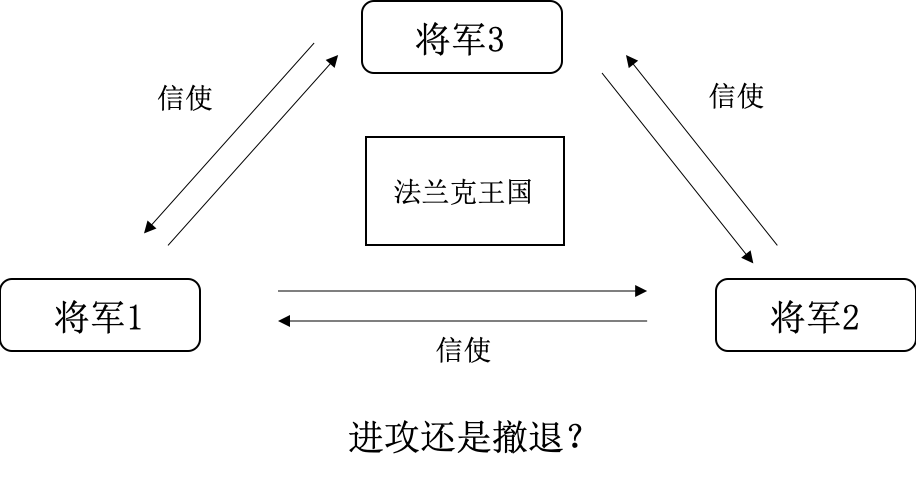
拜占庭将军的问题在于，将军中可能出现叛徒。假设3名将军中有1名叛徒，2名忠诚将军一人投进攻票，一人投撤退票，这时叛徒可能会故意给投进攻的将军投进攻票，而给投撤退的将军投撤退票。这就导致一名将军带队发起进攻，而另外一名将军带队撤退。

另外，由于将军之间通过信使进行通讯，即使所有将军都忠诚，也不能排除信使被敌人截杀，甚至信使叛变等情况。

假设存在叛变将军或信使出问题等情况，如果忠诚将军仍然能够通过投票来决定他们的战略，便称系统达到了拜占庭容错（Byzantine Fault Tolerance）。

拜占庭问题对应到区块链中，将军就是节点，信使就是网络等通信系统，要解决的是存在恶意节点、网络错误等情况下系统的一致性问题。

PBFT（Practical Byzantine Fault Tolerance） 是第一个得到广泛应用且比较高效的拜占庭容错算法，能够在节点数量不小于 $n=3f+1$ 的情况下容忍 $f$ 个拜占庭节点（恶意节点）。

1.4、区块链的分叉

即使区块链是可靠的，现在还有一个问题没有解决：如果两个人同时向区块链写入数据，也就是说，同时有两个区块加入，因为它们都连着前一个区块，就形成了分叉。这时应该采纳哪一个区块呢？

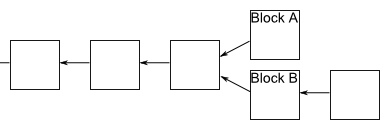
现在的规则是，新节点总是采用最长的那条区块链。如果区块链有分叉，将看哪个分支在分叉点后面，先达到6个新区块（称为”六次确认”）。按照10分钟一个区块计算，一小时就可以确认。

由于新区块的生成速度由计算能力决定，所以这条规则就是说，拥有大多数计算能力的那条分支，就是正宗的区块链。

1.5、总结

区块链作为无人管理的分布式数据库，从2009年开始已经运行了12年，没有出现大的问题。这证明它是可行的。

但是，为了保证数据的可靠性，区块链也有自己的代价。一是效率，数据写入区块链，最少要等待十分钟，所有节点都同步数据，则需要更多的时间；二是能耗，区块的生成需要矿工进行无数无意义的计算，这是非常耗费能源的。

因此，区块链的适用场景，其实非常有限。

1. 不存在所有成员都信任的管理当局
2. 写入的数据不要求实时使用
3. 挖矿的收益能够弥补本身的成本

如果无法满足上述的条件，那么传统的数据库是更好的解决方案。

二、以太坊介绍

2.1、以太坊简介

以太坊是一个开放的区块链平台，允许任何人在平台中建立和使用通过区块链技术运行的去中心化应用，同比特币一样，以太坊由全球范围的很多人共同创建，不受任何个人控制。

2.1.1、下一代区块链

区块链技术是比特币的底层技术。在比特币中，分布式数据库被设想为一个账户余额表（总账），交易通过比特币的转移来实现个体之间无需信任基础的金融活动。以太坊试图实现一个总体上完全无需信任基础的智能合约平台。

2.1.2、以太坊虚拟机

以太坊是可编程的区块链，不会给用户一系列预先设置好的操作，允许用户自定义复杂的操作。以太坊狭义上是指一系列定义去中心化应用平台的协议，核心是以太坊虚拟机（EVM），其可以执行任意复杂算法的编码。以太坊是图灵完备的。

以太坊也有一个点对点的网络协议，以太坊区块链数据库由各网络节点来维护和更新，每个节点运行以太坊虚拟机并执行相同的指令，保证区块链的一致性。

2.1.3、以太坊工作原理

比特币可以看作是关于交易的列表，而以太坊的基础单元是账户。以太坊跟踪每个账户的状态，以太坊上所有状态转换都是账户之间价值和信息的转换。

账户分为两类：

• 外部账户（EOA）：由私人密钥控制
• 合约账户：由合约代码控制，只能由外部账户“激活”。

智能合约：指合约账户中的编码，即交易被发送给该账户时所运行的程序。用户可以通过在区块链中部署编码来创建新的合约。

只有当外部账户发出指令时，合约账户才会执行相应的操作，是为了保证正确执行所有操作。

和比特币一样，以太坊用户需要向网络支付少量的交易费用，通过以太币的形式支付。这样避免受到类似DDos的攻击。

交易费用由节点收集，节点使网络生效。“矿工”就是以太坊网络中收集、传播、确认和执行交易的节点。矿工将交易打包，打包的数据成为区块，打包的过程就是将以太坊中账户的状态更新的过程。矿工们相互竞争挖矿，成功挖矿的可以得到以太币的奖励。

2.1.4、幽灵协议

幽灵合约的英文是“Greedy Heaviest Observed Subtree” (GHOST) protocol，在介绍幽灵协议之前，先介绍以太坊中的叔区块、叔块奖励和叔块引用奖励这三个概念。

假设目前以太坊区块链中的区块高度（区块链上的区块个数）为6，现在产生了一笔新的交易，矿工A先将该笔交易打包成了区块 Block 7，在矿工A将 Block 7 广播到其他节点的这段时间里，矿工B和矿工C又分别产生了 Block 8 和 Block 9。Block 7、Block 8、Block 9 都指向 Block 6，即 Block 6 是他们的父区块。由于 Block 7 是最先产生的，因此 Block 7 被认为是有效区块，Block 8 和 Block 9 就是叔区块（作废区块）。

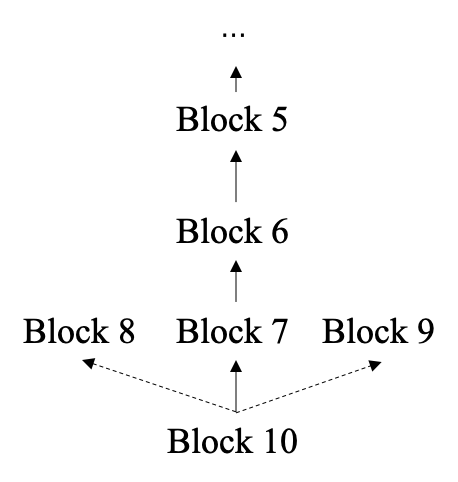
现在链上的区块高度为7，在这基础上又产生了新的交易，并被打包成了 Block 10。在以太坊中，Block 10 除了可以引用它的父区块 Block 7 外，还可以引用叔区块 Block 8 和 Block 9。并且，Block 8 和 Block 9 的矿工会因此获得一笔奖励，称为叔块奖励，Block 10 的矿工除了基础奖励之外，由于引用了叔区块，还会获得一笔额外的叔块引用奖励。

幽灵协议是以太坊的一大创新。由于在比特币中的出块时间被设计为10分钟，而以太坊为了提高出块速度，将出块时间设计为12秒（实际14~15秒左右），这样的高速出块意味着高速确认，高速确认会带来区块的高作废率和低安全性。因为区块需要花一定的时间才能广播至全网，如果矿工 A 挖出了一个区块，而矿工 B 碰巧在 A 的区块扩散至 B 之前挖出了另一个区块，矿工 B 的区块就会作废并且没有对区块链的网络安全做出贡献。此外，这样的高速确认还会带来中心化的问题：如果 A 拥有全网 30% 的算力而 B 拥有 10% 的算力，那么 A 将会在 70% 的时间内都在产生作废区块，而 B 在 90% 的时间内都在产生作废区块，这样，B 永远追不上 A，后果是 A 通过其算力份额拥有对挖矿过程实际上的控制权，出现了算力垄断，弱化了去中心化。

幽灵协议正是为了解决上述问题而引入的，协议的主要内容如下：

• 计算最长链时，不仅包括当前区块的父区块和祖区块，还包括祖先块的作废的后代区块（叔区块），将它们综合考虑来计算哪一个区块拥有支持其的最大工作量证明。这解决了网络安全性的问题
• 以太坊付给以“叔区块”身份为新块确认作出贡献的废区块87.5%的奖励（叔块奖励），把它们纳入计算的“侄子区块”将获得奖励的12.5%（叔块引用奖励）。这就使得即使产生作废区块的矿工也能够参与区块链网络贡献并获得奖励，解决了中心化倾向的问题
• 叔区块最深可以被其父母的第二代至第七代后辈区块引用。这样做是为了：
  • 降低引用叔区块的计算复杂性
  • 过多的叔块引用奖励会剥夺矿工在主链上挖矿的激励，使得矿工有转向公开攻击者链上挖矿的倾向（即公开攻击者可能会恶意产生大量作废区块，无限引用将会诱使矿工转移到攻击者的链上，从而抛弃合法的主链）
  • 计算表明带有激励的五层幽灵协议即使在出块时间为15s的情况下也实现了了95%以上的效率，而拥有25%算力的矿工从中心化得到的益处小于3%

2.1.5、以太坊的组成部分

在以太坊中，包括了 P2P 网络、共识机制、交易、状态机、客户端这几个组成部分。

• P2P 网络：在以太坊主网上运行，可通过TCP端口30303访问，并运行称为 ÐΞVp2p 的协议。
• 共识机制：以太坊目前使用名为 Ethash 的 POW 算法，计划在将来会过渡到称为 Casper 的 POS 算法。
• 交易：以太坊中的交易本质上是网络消息，包括发送者、接收者、值和数据载荷（payload）。
• 状态机：以太坊的状态转移由以太坊虚拟机（Ethereum Virtual Machine，EVM）处理，EVM 能够将智能合约编译成机器码并执行。
• 客户端：用于用户和以太坊进行交互操作的软件实现，最突出的是 Go-Ethereum(Geth) 和 Parity。

2.1.6、以太坊中的概念

• 账户：以太坊中的账户类似于银行账户、应用账户，每个账户有一个20字节的地址。账户又分为普通账户（又叫外部账户，External Owned Account, EOA）和合约账户（Contract）。普通账户是由以太坊使用者创建的账户，包含地址、余额和随机数；合约账户是创建智能合约时建立的账户，包含存储空间和合约代码
• 状态：状态是由账户和两个账户之间价值的转移以及信息的状态转换构成的
• 地址：地址是一个账户 ECDSA 公钥的 Keccak 散列最右边的160位，通过地址可以在以太坊上接收或发送交易。在 Etherscan 上，可以通过地址来查询一个账户的信息
• 交易：以太坊中的交易不仅包括发送和接收以太币，还包括向合约账户发送交易来调用合约代码、向空用户发送交易来生成以交易信息为代码块的合约账户
• Gas：Gas 是以太坊中的一种机制，用于执行智能合约或交易操作的虚拟燃料。由于以太坊是图灵完备的，为了避免开发者无意或恶意编写出死循环等浪费资源或滥用资源的情况，以太坊中的每一笔交易都需支付一定的 Gas （燃料费），即需支付一定的以太币作为 Gas。Gas 的金额通常是由交易的发起者指定并支付的
• 挖矿：和比特币类似，以太坊同样通过挖矿来产生区块。在以太坊目前的 PoW 机制下，每当一笔交易发出并广播，就会吸引矿工来将该交易打包成区块。每产生一个区块都会有一笔固定奖励给矿工，目前的固定奖励是3个以太。同时，区块中所有操作所需的 Gas 也会作为奖励给矿工。与比特币不同的是，以太坊中产生叔块的矿工可能会获得叔块奖励，引用叔块的矿工会获得叔块引用奖励
• DApp（去中心化应用）：通过智能合约，开发者能够设计想要的逻辑，相当于是网站的后端。而 DApp 则相当于是一个完整的网站（前端+后端），因此 DApp = 智能合约 + Web 前端。以太坊提供了一个名为 web3.js 的 Javascript 库，通过 web3.js 可以实现 Web 与以太坊区块链的交互和与智能合约的交互，方便开发者创建 DApp

2.2、以太坊账户管理

2.2.1、账户

以太坊有两种账户类型：

• 外部账户（EOA）
• 合约账户

所有账户的状态代表以太坊网络的状态，以太坊网络会和每一个区块一起更新，网络需要达成关于以太坊的共识。账户代表外部代理人的身份，账户运用非对称加密的私钥来签署交易，以便以太坊虚拟机可以安全验证交易发送者的身份。

2.2.2、钥匙文件(Keyfiles)

每个账户都由一对密钥来定义，包括公钥和私钥。账户以地址为索引，地址由公钥生成，每对私钥/地址都编码在一个钥匙文件（JSON文件）中，其中最重要的为账户私钥，通常用创建账户时的密码加密。可以在以太坊节点数据目录的keystore子目录下找到钥匙文件。

2.2.3、创建账户

为了从账户发送交易包括以太币，需要拥有Keyfiles和密码。需要记住并备份钥匙文件，没有“找回密码”的选项。

参考资料

DataWhale 区块链教程

区块链入门教程

RSA算法原理（一）

RSA算法原理（二）

比特币入门教程

密码学笔记

数字签名是什么？

How does blockchain really work?, by Sean Han

Bitcoin mining the hard way: the algorithms, protocols, and bytes, by Ken Shirriff

Merkle Tree及其实现

以太坊系列（一）之以太坊介绍

以太坊系列（二）之账户管理

胡伟煌个人博客